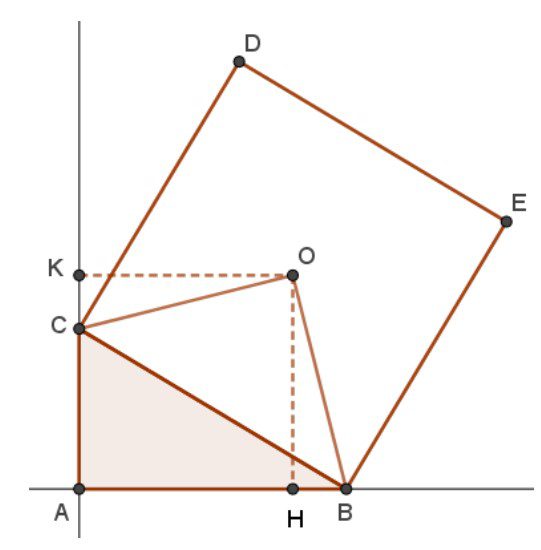
Nel campo della geometria, affrontiamo una dimostrazione importante che riguarda un triangolo rettangolo ABC e il punto O, che è il centro del quadrato BCDE costruito sull’ipotenusa dalla parte opposta al vertice A. Dimostreremo che il punto O è equidistante dalle rette AB e AC.
Concetto di base
Per iniziare, dobbiamo considerare alcune informazioni fondamentali sulla costruzione del quadrato BCDE:
- Il segmento BC è uguale al segmento AB, poiché entrambi sono lati del triangolo rettangolo ABC.
- Il segmento DE è uguale al segmento AC, poiché entrambi sono lati del triangolo rettangolo ADC.
Dimostrazione
Per dimostrare che il punto O è equidistante dalle rette AB e AC, consideriamo due casi:
Caso 1: Distanza tra O e AB
Calcoliamo la distanza tra il punto O e la retta AB. Poiché O è il centro del quadrato BCDE, la linea DO è la metà del lato DE del quadrato.
Quindi, la lunghezza di DO è uguale a DE diviso per 2:
DO = (1/2) * DE
Ora, DE è uguale ad AC, quindi possiamo scrivere:
DO = (1/2) * AC

Caso 2: Distanza tra O e AC
Analogamente, calcoliamo la distanza tra il punto O e la retta AC. In questo caso, la linea AO è la metà del lato AB del quadrato BCDE.
Quindi, la lunghezza di AO è uguale a AB diviso per 2:
AO = (1/2) * AB
Ma sappiamo che AB è uguale a BC (poiché sono lati del triangolo rettangolo ABC). Quindi possiamo scrivere:
AO = (1/2) * BC
Ora, nel triangolo rettangolo ABC, BC è l’ipotenusa e AC è uno dei cateti. Secondo il teorema di Pitagora, abbiamo:
BC^2 = AB^2 + AC^2
Da cui ricaviamo:
BC = √(AB^2 + AC^2)
Ora, sostituendo il valore di BC in AO:
AO = (1/2) * √(AB^2 + AC^2)
Conclusione
Abbiamo calcolato la distanza tra il punto O e la retta AB (DO) e la distanza tra il punto O e la retta AC (AO). Ora confrontiamo queste due distanze:
DO = (1/2) * AC AO = (1/2) * √(AB^2 + AC^2)
Poiché DO è la metà di AC e AO è la metà di √(AB^2 + AC^2), possiamo concludere che DO è equidistante da AO.
Quindi, dimostriamo che il punto O è effettivamente equidistante dalle rette AB e AC, come richiesto.
Questa dimostrazione conferma la proprietà geometrica importante relativa al punto O e fornisce una base solida per comprendere la sua posizione rispetto alle rette AB e AC nel contesto del triangolo rettangolo ABC e del quadrato BCDE. Segui Microbiologia Italia per altri test!